Adının da işâret ettiği (Gnu's Not Unix!) üzere açık-kaynak hareketinin eski (1986) ve köklü yazılımlarından olan gnuplot, temel olarak komut satırından idâre edilen fonksiyon/veri çizim programıdır. Sâhip olduğu yetenekler sebebiyle dünya çapında bilim/mühendislik camiası tarafından yaygın olarak kullanılmaktadır, fakat Türkiye açısından aynısını ifâde etmek biraz zordur, zirâ pencereci ve de tencereciyiz biz...

Bu yazılımı, ilgilenebilecek olan gençlere ve geleceğin mühendis adaylarına biraz tanıtabilmek için birşeyler söylemek icâb ediyordu. Uygulamalı bir örnek verebilmek için de ilgi çekici olabilecek bir konu gerekliydi. Bu doğrultuda sitenin gidişâtı ile de bağlantılı "takviyesiz silindirik kabukların burkulması" hakkında yayınlamış bir veri dizisi gâyet uygun gözüküverdi.

 ♦ uçbirim:
wget http://alarga.uskudar.biz/dosyalar/noktalar.dat.tar.gz

İçeriğine bakıldığında görülebileceği gibi elimizde çeşitli yarıçap/kalınlık oranları için elde edilmiş denel burkulma yükü değerlerinin analitik çözüme oranlarını gösteren (x;y) düzeninde verilmiş ve boşluk/sekme ile ayrılmış 314 satır veri mevcut.

İşletim sisteminizde çalışan bir gnuplot sürümünün kurulu olduğunu ve çakma değil gerçek bir işletim sistemi kullandığınızı varsayarak devam edelim. Bu arada aşağıdaki örnek uygulamanın gnuplot 5.0 üzerinde çalıştırıldığını belirtelim. Şimdi doğrudan uçbirim üzerinden, söz konusu ham veriyi 2B olarak görüntüleyebiliriz:

 ♦ uçbirim:
gnuplot

 ♦ uçbirim:
gnuplot> set decimalsign locale; plot 'noktalar.dat'

Görüldüğü gibi komut iki temel bölümden oluşuyor; ilk bölüm veri dosyasına uygun olacak şekilde ondalık ayırıcının "," olarak tanımlanması ki Türkçe'ye ayarlı bir bilgisayar için bu komut sayesinde işlem otomatik olarak gerçekleşir. İkinci bölümde ise işâret edilen veri dosyası içindeki noktalar otomatik olarak bir X11 penceresi üzerine çizilir. Eğer bir sorun çıkmadıysa veri dağılımının çizimini görebilmiş olmanız gerekir.

 ♦ gnuplot:
# gnuplot ile eğilimeğrisi - http://alarga.uskudar.biz
# Bütün giriş-çıkışlar için Türkçe ondalık ayırıcının "," olarak tanıtılması
set decimalsign locale; set decimalsign "."
 
set title "Takviyesiz Silindirik Kabuklar için Burkulma Yükleri"
set grid                              # artalan ızgarası
set xlabel "r / t"                    # X-ekseni başlığı
set ylabel "P_{deney} / P_{hesap}"    # Y-ekseni başlığı
set xrange [0:4250]                   # X-ekseni aralığının ayarlanması
set yrange [0:1]                      # Y-ekseni aralığının ayarlanması
set xtics 0,500,4000                  # X-ekseni aralıkları için özel ayar
 
set termoption enhanced
f1(x) = a*log10(x) + b                # Logaritmik eğilimeğrisi
  fit f1(x) 'noktalar.dat' via a,b
 
f2(x) = c + d*x + e*x**2 + f*x**3     # 3.derece Polinom eğilimeğrisi
  fit [25:4250] f2(x) "noktalar.dat" via c,d,e,f
 
f3(x) = g*x**h;                       # Üstel eğilimeğrisi
  fit f3(x) "noktalar.dat" via g,h
 
plot 'noktalar.dat' with points pointtype 6 pointsize 1 title 'veri noktaları', \
  f2(x) with lines linewidth 1.5 linecolor 7 title sprintf('f(x) = %.2f %.3g·x+%.3g·x^2 %.3g·x^3', c,d,e,f), \
     f1(x) with lines linewidth 2.0 linecolor 2 title sprintf('f(x) = %.3f·log10(x) + %.3f', a,b), \
  f3(x) with lines linewidth 1.5 linecolor 4 title sprintf('f(x) = %.4f·x^{%.5f}', g,h)
 
pause mouse close    # gnuplot-X11 çizim penceresinin açık kalması için

gnuplot: burkulmaOranları

Gnuplot doğrudan ve tam işlevli olarak sadece komut satırı üzerinden idâre edilebilir. Bununla birlikte bâzı durumlarda önceden ayarlanmış bir betik dosyası üzerinden kullanılması daha verimli olabilmektedir.

Hemen yukarıda verilen gnuplot betiğinin içeriği, "burkulmaOranları" veya keyfinize göre herhangi bir isimde adlandırılmış boş bir metin dosyasının (dosya uzantısına gerek yok) içine yapıştırıldığında işlem tamam sayılır. Geriye çalıştırmak kalıyor:

 ♦ uçbirim:
gnuplot burkulmaOranları

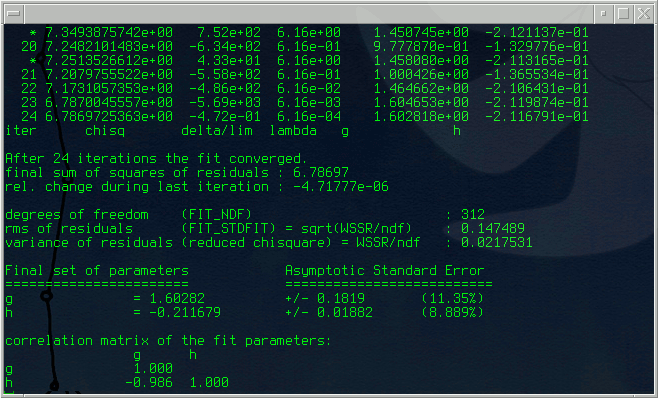
Olağan şartlarda, saniyeler içinde aşağıdaki [Resim.1] görüldüğü gibi uçbirim penceresinde işlemin doğru olarak sonuçlandığını ve açılan yeni bir pencerede de betik ile talep edilen çizimin nihaî hâlini [Resim.2] görebilmeniz gerekir.

Resim.1) Yukarıdaki betik için, uçbirim penceresinin son satırları. Eğilim çizgileri için gerçekleşen hesapların ayrıntıları aynı dizin içinde otomatik olarak oluşacak olan "fit.log" dosyası içinde görülebilir.

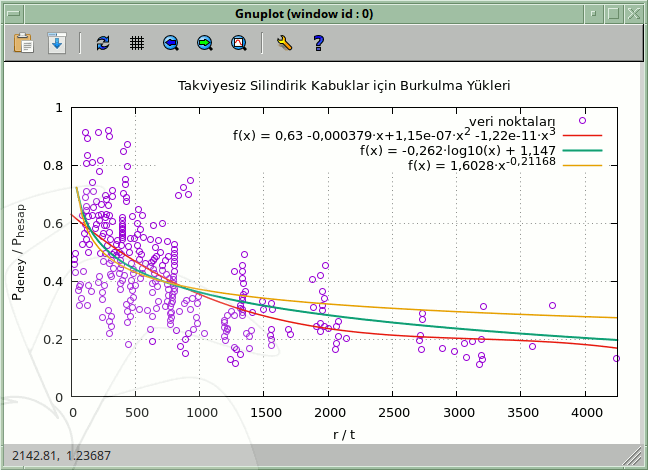
Resim.2) "burkulmaOranları" betiği ile elde edilen sonuç. Veri noktalarının dağılımı, üç farklı yöntem (3. derece Polinom, Logaritmik ve Üstel) ile elde edilen eğilimeğrileri ve bu eğrilerin eşitlikleri ile birlikte. Betik üzerinde değişiklik yaparak etkilerini görmek size kalmış...
Bu X11 penceresi üzerinde fare ile yakınlaştırma, kaydırma ve istenen bir noktadan veri alma, çizimin *.png, *.pdf veya *.svg olarak ihracı vesaire gerçekleştirilebilir.

Bu örnek çalışmada kullanılan temel veri, kaynak [3] üzerindeki bir grafikten geri kazanılmıştı. Söz konusu resim dosyasından sayısal verilerin alınması için ise g3data adlı bir başka yazılım kullanılmıştır ki bu yazılımı merak edenler [4]'e göz atabilir.

Şimdi elimizdeki bu veriye biraz da asıl yönüyle bakarsak, geometrik kusurların burkulma hususunda ne kadar önemli bir ayrıntı olduğunu da kavramış oluruz. Bu grafik eksenel yük altında, muhtelif yarıçap/kalınlık oranındaki, hafifçe şekil kusurlarına sahip silindirik yapıların deneylerle elde edilen sonuçları ile nazari çözümlerle elde edilen burkulma yükü değerleri arasında ne kadar büyük farklar olabildiğini de açıkça göstermektedir. Yükleme ve sınır şartlarının türleri de kusur hassasiyetin seviyesi üzerinde büyük bir etkiye sahiptir.

Herhangi bir imalât sonucunda geometrik kusurlar oluşması kaçınılmazdır. Bununla birlikte bu kusurların sınırlarını bilebilmek ve uygulayabilmek de hayâti önem taşımaktadır. Biraz daha somut bir örnek vermek ve kabaca ifâde etmek gerekirse, denizaltı mukavim tekneleri üzerinde enine doğrultuda, çapın %0,3'ü kadar bir kusur azamî dalış derinliğinin üçte birinin kaybedilmesi anlamına gelebilir ki mesela 6,2m çapındaki bir Tip209/214 gövdesi için bu ~19mm'den ibârettir.