| Ufuk |
| Pazar, 17 Ocak 2021 |
|
Konunun bu ilk safhasında, ihtiyacı karşılayarak yeterli sayılabilecek bir hassasiyette çözüm elde edebilmek için aşağı yukarı ilkokul matematiği yeterli olacaktır ki söz konusu mevzu; deniz üzerinde ufuk hattı mesâfesinin hesaplanması, hakkındadır. Bahsi geçen ufuk çizgisi geometrik ve elektromanyetik açılardan farklılıklar gösterdiği için adım adım ilerlemek daha uygun olur. 
Resim.1) Sayfanın temel içeriğini tanımlamakta ve aşağıdaki hesaplamalarda kullanılacak ölçeksiz yerküre taslağı. Enleme bağlı olarak bir miktar değişiklik gösterse de yerkürenin ortalama yarıçapı 6.371,0km olarak kâbûl edilebilir. Ekvator üzerinde yarıçap 6.378,137km, kutup yarıçapı ise 6.356,752km'dir. Resim üzerinde fare tekerliği ile yaklaşmak ve fare ile sürüklemek de mümkündür... Karalardan, diğer suüüstü yapılarından ve araçlarından tamamen uzakta, sıfır deniz durumunda, hareketsiz olarak su üstünde durmakta olan bir gemi kurgulayalım, [Resim.1] üzerinde görüldüğü gibi. Şimdi bu geminin direğinin tepesine yerleştirilmiş radarına ait ufuk mesafesini hesaplamaya çalışalım. Geometrik UfukSuhattından [y1] mesafesinde [B] noktasına yerleştirilmiş radardan yayılan bir elektromantetik ışının tamamen doğrusal bir yol izleyeceği kabûl edilirse bu ışın alt sınır olarak yerküreye [C] noktasında teğet olur ki bu durumda söz konusu teğet noktasını yerkürenin merkezine bağlayan yarıçap çizgisi [Ryer] ile radar ışınını tanımlayan [BC] doğrusu birbirlerine dik açı teşkil eder. Bu şartlar altında [M,C,B] noktaları bir dik üçgen oluşturacaktır. Hâliyle, gemi üzerindeki radarın "geometrik ufku" (sarı) şimdi kolayca hesaplanabilir: $$ \begin{aligned} BC^{2} = MB^{2} - MC^{2} \end{aligned} $$ MB doğrusu (Ryer + y1)'den ve MC doğrusu da Ryer'den ibâret olduğuna göre: $$ \begin{aligned} BC = \sqrt{2\cdot R_{yer}\cdot y1 + y1^{2}} \end{aligned} $$ Bir örnek olması açısından mesele sayıya dökülüp TCG Heybeliada'nın direği üzerinde iken Smart-S radarının geometrik ufkunun radara mesafesi hesaplanırsa: $$ \begin{aligned} BC = \sqrt{2\cdot 6.371\cdot 0,0256 + 0,0256^{2}} = 18,06km \end{aligned} $$ olarak ortaya çıkar. Aslına bakılırsa [y1] [Ryer]'ye göre çok çok küçük1 olduğundan ihmâl edilebilir ki böylece yukarıdaki eşitlik: $$ \begin{aligned} BC = 3,57155\sqrt{y1} \end{aligned} $$ hâlinde de kullanılabilir, [y1] metre ve sonuç kilometre olmak üzere. Elektromanyetik UfukFakat hava, elektromanyetik dalgaların kırılmasına sebep olur ve bu kırılmanın oluşumu ve etkileri dalgaboyuna da doğrudan bağlıdır, dolayısıyla mesela radar ve ışık farklı şekilde etkilenir. Şimdilik konu radar temelindedir ve radarlar içinden de ancak gemiler üzerinde kullanılagelen yüksek frekans bantlarında çalışanlar içeriğin merkezindedir. Alçak frekanslı özel radarları, görünür veya görünmez dalgaboylarındaki optik araçları, bu açıdan ayrıca ele almak daha uygun olur. Nihâyetinde bahsi geçen kırılma sebebiyle, bir önceki altbaşlıkta kullanılan; radar ışınının düz bir hat üzerinde hareket ettiği kabûlü, uygunsuz bir hâle düçâr olur. Velhâsıl havaküre kaynaklı etkiler gerçek radar ufkunun mesafesi üzerinde göz ardı edilemeyecek sapmalar meydana getirir. Atmosfer şartlarına bağlı olarak gerçek radar ufku çoğunlukla yukarıda hesaplanan geometrik ufuktan daha uzakta, bâzen de daha yakında oluşur. Radar UfkuGemi radarları açısından hızlı bir yaklaşık çözüm elde etmek için ampirik yaklaşımlar kullanılır. Bunlar içinde en yaygını ortalama kırılma etkisine karşılık gelebilecek bir [k] katsayısını yukarıda eşitliğe ilâve ederek BD yayını hesaplamaktan ibârettir. $$ \begin{aligned} BD = 3,57155\sqrt{k\cdot y1} \end{aligned} $$ ki k=4/3 için eşitlik şu hâle gelir: $$ \begin{aligned} BD = 4,124\sqrt{y1} \end{aligned} $$ Deniz yüzeyinin üstündeki bir cismin irtifasına bağlı olarak bu cismin gemi radarı tarafından tespit edilebileceği [E] noktası için âzamî ufuk menzili ise şu şekilde hesaplanabilir: $$ \begin{aligned} BE = 4,124(\sqrt{y1}+\sqrt{y2}) \end{aligned} $$ Yine yukarıdaki gibi bir sayısal örnekle devam edilirse 3m irtifada uçarak gemiye yaklaşmakta olan gemisavar güdümlü mermiyi Heybeliada Sınıfı bir geminin tespit edebileceği mesafe yaklaşık olarak: $$ \begin{aligned} BE = 4,124(\sqrt{25,6}+\sqrt{3,0}) = 28,01km \end{aligned} $$ olarak tahmin edilebilir, tabii gemi radarının örnek füzenin RKA'sına2 yetecek güçte olduğu varsayılırsa. 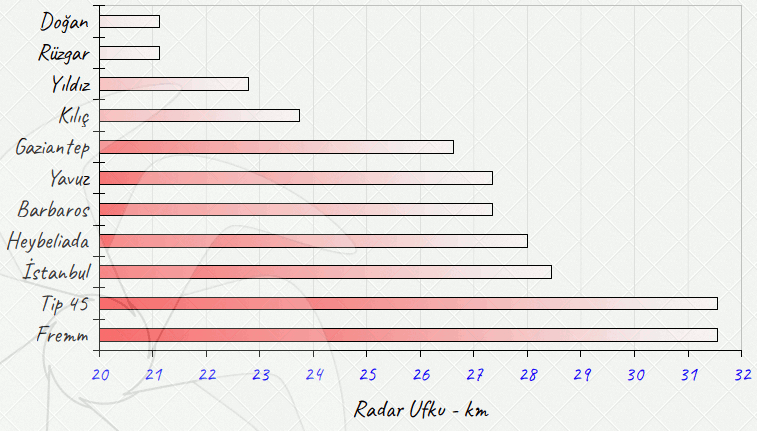
Resim.2) Türk Donanmasının başlıca suüstü unsurlarının yukarıdaki ampirik yaklaşım ile hesaplanmış, 3m irtifadaki bir cisme karşı radar ufuklarının mesafeleri ve bir fikir vermesi açısından Tip45 ve Fremm Sınıfı gemilerle karşılaştırılması. İkinci bölümde dalga kırılmasının etkilerini ayrıntılı olarak el almak düşünülüyor çünkü gerçek şartlarda ortaya çıkacak durumlar aslında son derece karmaşıktır ve konu gemi savunması açısından çok önemlidir. Yaftalar: |