Geçtiğimiz Nisan ayında Elmer'in 8.4 sürümünün yayınlanmasıyla birlikte, diğer bâzı yenilikler ve iyileştirmeler yanında bu zamana kadar eksikliği hissedilen iyi bir cidar çözücüsü yönünde önemli bir adım da atılmış oldu. Söz konusu çözücünün yeteneklerini kavrayabilmek için ilk olarak halka şeklinde ince bir levhadan müteşekkil olan bir yapının doğal frekanslarının incelenmesi ve yöntem doğrulanması çalışmaları için hazırlanmış olan Afnor SDLS04/89 [1] tercih edildi.

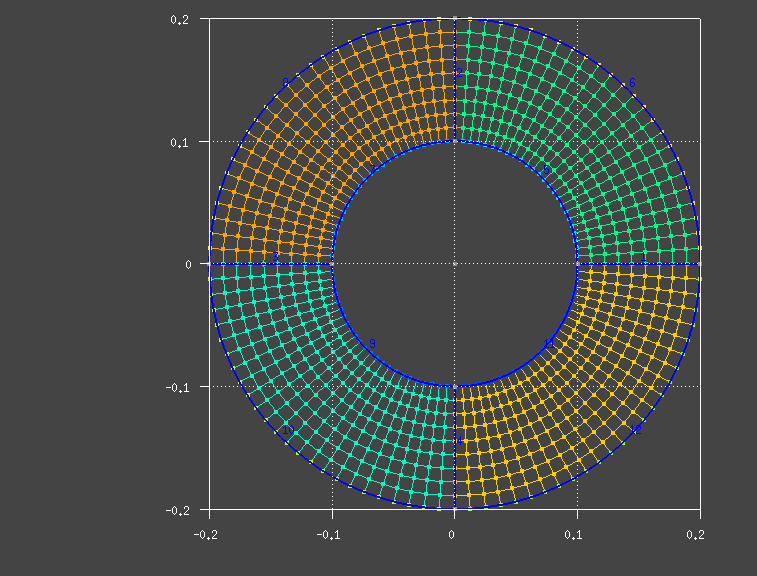
Resim.1) Aşağıda verilen Gmsh betiği ile SDLS04-89 çözümü için birinci derece 2B cidar elemanları ile hazırlanan hesaplama örgüsü. Buradaki çözünürlük; k=2 (2x)

Dış yarıçapı 0,2m ve iç yarıçapı 0,1m olan, 1mm kalınlığındaki dairevi bir halkadan ibaret cisim, iç kenarından sabit olarak mesnetlenmiştir. Aşağıdaki betik vasıtasıyla ilgilenen ziyaretçiler Gmsh yazılımı kullanarak bu cismi cidar elemanlarıyla 2 boyutlu olarak üretip kullanabilirler. Bu vesileyle, "Transfinite" yaklaşımı kullanılarak nasıl düzenli örgü oluşturulabileceği de örnek olarak gösterilmiş oldu ki eşdeğer bir örgü farklı yöntemlerle de imâl edilebilirdi.

 ♦ gmsh:
// SDLS04/89
// http://alarga.uskudar.biz
ri = 0.10;  // iç yarıçap, metre
rd = 0.20;  // dış yarıçap
k = 2;      // çözünürlük katsayısı
 
dd = k*13;
dh = k*5;
Point (0) = {0, 0, 0};  // merkez
Point (1) = {ri, 0, 0};
Point (2) = {rd, 0, 0};
Point (3) = {0, ri, 0};
Point (4) = {0, rd, 0};
Point (5) = {-ri, 0, 0};
Point (6) = {-rd, 0, 0};
Point (7) = {0, -ri, 0};
Point (8) = {0, -rd, 0};
  Line (1) = {1,2};
  Line (2) = {3,4};
  Line (3) = {5,6};
  Line (4) = {7,8};
  Circle (5) = {1,0,3};
  Circle (6) = {2,0,4};
  Circle (7) = {3,0,5};
  Circle (8) = {4,0,6};
  Circle (9) = {5,0,7};
  Circle (10) = {6,0,8};
  Circle (11) = {7,0,1};
  Circle (12) = {8,0,2};
// ilk çeyrek
Transfinite Line(1) = dh Using Progression 1;
Transfinite Line(2) = dh Using Progression 1;
Transfinite Line(5) = dd Using Progression 1;
Transfinite Line(6) = dd Using Progression 1;
  Line Loop (1) = {1,6,-2,-5};
  Plane Surface (1) = {1};
  Transfinite Surface (1) = {1,2,3,4};
  Recombine Surface (1);
// ikinci çeyrek
Transfinite Line(2) = dh Using Progression 1;
Transfinite Line(3) = dh Using Progression 1;
Transfinite Line(7) = dd Using Progression 1;
Transfinite Line(8) = dd Using Progression 1;
  Line Loop (2) = {2,8,-3,-7};
  Plane Surface (2) = {2};
  Transfinite Surface (2) = {3,4,5,6};
  Recombine Surface (2);
// üçüncü çeyrek
Transfinite Line(3) = dh Using Progression 1;
Transfinite Line(4) = dh Using Progression 1;
Transfinite Line(9) = dd Using Progression 1;
Transfinite Line(10) = dd Using Progression 1;
  Line Loop (3) = {3,10,-4,-9};
  Plane Surface (3) = {3};
  Transfinite Surface (3) = {5,6,7,8};
  Recombine Surface (3);
// dördüncü çeyrek
Transfinite Line(1) = dh Using Progression 1;
Transfinite Line(4) = dh Using Progression 1;
Transfinite Line(11) = dd Using Progression 1;
Transfinite Line(12) = dd Using Progression 1;
  Line Loop (4) = {4,12,-1,-11};
  Plane Surface (4) = {4};
  Transfinite Surface (4) = {1,2,7,8};
  Recombine Surface (4);
 
Mesh.ElementOrder = 1;  // yalnızca 1.derece eleman kullanılabilir
 
// Elmer için adlandırmalar
Physical Surface("1") = {Surface "*"};
Physical Line("2") = {5,7,9,11};

Gmsh: halkaLevha.geo

Gmsh'den (burada 3.0.6 kullanıldı) Elmer yazılıma yönelik en uygun örgü ihracı *.msh dosya biçimi ile gerçekleştirilebilir. Dolayısıyla yukarıdaki betik kullanılarak 2B ve 1.derece örgü [Resim.1] üretildikten sonra mesela "halkaLevha.msh" olarak ihraç edilir ve bunu yaparken "version 2.0 ASCII" tercihi uygun olur, bu safhada diğer seçenekler ise işaretlenmemelidir.

Elmer (burada 8.4 kullanıldı) ile söz konusu hesaplama örgüsünü kullanabilmek için bir dönüştürme işlemine ihtiyaç vardır. Bu işlem için ise uçbirim üzerinde çalışan ElmerGrid¹ adlı araç kullanılır;

 ♦ uçbirim:
ElmerGrid 14 2 halkaLevha.msh -autoclean

Bu ifadede "14" giriş dosyasının türünü (burada Gmsh'den gelen *.msh anlamında) "2" çıkış dosyasının türünü (burada ElmerSolver anlamında) tanımlamaktadır, devamında dönüştürülecek dosyanın adı girilmiştir ve "-autoclean" ise bu işlem esnasında ihtiyaç duyulmayan artık verilerin temizlenmesini sağlar. Nihayetinde, giriş doyası ile aynı isimdeki dizin içinde Elmer tarafından kullanılmaya uygun hesaplama örgüsü elde edilmiş olur. Söz konusu dizin içinde aşağıdaki bileşenler mevcut olacaktır:

1. entities.sif
2. mesh.boundary
3. mesh.elements
4. mesh.header
5. mesh.names
6. mesh.nodes

Bu safhadan sonra iki farklı yol ile devam edilebilir. Bunlardan ilki ELmerGUI adlı grafik arayüzü kullanarak yukarıdaki örgü dosyasını (daha doğrusu dizinini) açıp çözüm ayarları için tıklayarak yola devam etmektir. Bununla birlikte ben bu yöntemi pek sevemedim, dolaysı ile şimdilik ikinci yoldan devam edelim.

İlk olarak yukarıdaki örgü dizini içinde burada "halkaCidar.sif" olarak adlandırlacak boş bir metin dosyası oluşturulur. Elmer için gerek duyulan bütün çözücü ayarları bu *.sif dosyası üzerinden idâre edilmektedir. Başlangıç için bu yaklaşım biraz zahmetli gibi görünse de aslında hem çok daha hızlı ve etkin çalışmayı hem de zaman içinde yazılımın yeteneklerine daha iyi hâkim olabilmeyi sağlayabilmektedir.

 ♦ elmer:
! SDLS04/89
! 2B cidar elemanları ile doğal frekans çalışması
! http://alarga.uskudar.biz
 
Check Keywords "Warn"
 
Header
  Mesh DB "." ""
End
 
! Benzetimin tanımlanması
Simulation
  Max Output Level = 6
  Coordinate System = Cartesian 3D
  Simulation Type = Steady
  Steady State Max Iterations = 1
End
 
! Katı cismin tanımlanması
Body 1
  Equation = 1
  Material = 1
End
 
! Gereken malzeme değişkenlerinin tanımlanması
! Hesaplama örgüsüne de uyumlu olarak SI birim sistemine göre
Material 1
  Density = 7800
  Shell Thickness = 0.001
  Youngs Modulus = 210e9
  Poisson Ratio = 0.3
End
 
Equation 1 :: Active Solvers(1) = 1 2
 
! Cidar çözücüsü ayarları
! İlk 21 mod için "Doğrudan" çözücü ile
Solver 1
  Equation = "Shell equations"
  Procedure = "ShellSolver" "ShellSolver"
  Variable = U
  Displace Mesh = False
  Linear System Solver = Direct !"Iterative"
 
  ! Eğer kullanılırsa "Yakınsamalı" çözücü ayarları
  Linear System Preconditioning = ILU2
  Linear System Max Iterations = 1000
  Linear System Convergence Tolerance = 1e-7
  Linear System Iterative Method = GCR
  Linear System GCR Restart = 300
  Linear System Abort Not Converged = False
  Steady State Convergence Tolerance = 1e-09
 
  ! Temel Eigen ayarları
  Eigen Analysis = True
  Eigen System Values = 21
  Eigen System Convergence Tolerance = Real 1.0e-6
  Eigen System Select = Smallest Magnitude
End
 
! Hesaplanan frekans değerlerinin dosyaya yazılması
! Sonuçlar özdeğerdir, ayrıca frekansa dönüştürülmeleri gerekir
Solver 2
  Equation = "SaveScalars"
  Filename = f.dat
  Procedure = "SaveData" "SaveScalars"
  Save EigenValues = Logical True
  Show Norm Index = 1
End
 
! Kartezyen koordinat sistemine göre
! Sınır şartlarının tanımlanması
! İç kenar (burada "1" olarak tanımlı) sabit mesnet
Boundary Condition 1
  Target Boundaries(1) = 1
  U 1 = Real 0  ! x yönünde yerdeğiştirme
  U 2 = Real 0  ! y yönünde yerdeğiştirme
  U 3 = Real 0  ! z yönünde yerdeğiştirme 
  U 4 = Real 0  ! x ekseni etrafında dönme
  U 5 = Real 0  ! y ekseni etrafında dönme
  U 6 = Real 0  ! z ekseni etrafında dönme
End

Elmer: halkaCidar.sif

Hemen yukarıda verilen numune .sif dosyasının içeriği olduğu gibi kopyalanıp daha önce oluşturulan henüz boş "halkaCidar.sif" içine yapıştırıldığında artık çözüm için hazır duruma gelinmiş olur. Tanımlanan problemi çözmek için atılması gereken son adım:

 ♦ uçbirim:
ElmerSolver halkaCidar.sif

Eğer uygun bir işletim sistemi üzerinde güncel Elmer sürümüne sahip bir bilgisayar ile çalışıyorsanız, uçbirim penceresi içinde çözümün ilerleyerek birkaç saniye içinde tamamlandığını görebilirsiniz.

Herhangi bir sorun çıkmadıysa aynı dizin içinde, çözücü içinde yapılan ayarlara bağlı olarak talep edilen "f.dat" ve "f.dat.names" adlı iki yeni sonuç dosyası oluşacaktır ki bunlar verilen cismin en küçük ilk yirmibir özdeğerinden ibarettir. Burada sadece doğal frekans değerlerine odaklandığımız için mod şekillerinin görüntülenebileceği sonuç dosyaları oluşturulmadı.

Fakat şunu da belirtmek gerekli ki Elmer frekans (f) değerlerini değil özdeğerleri (c) beyan etmektedir. Bu durumda son olarak, hesaplanan özdeğerlerin (eigendeğeri) frekanslara (Hz) dönüştürülmesi gerekir:

$$ \Large f = \frac{\sqrt{c}}{2\pi} $$

Çizelge.1) Yukarıda verilen Gmsh betiği üzerindeki k değişkenine [1, 2, 3, 4, 5] bağlı olarak beş farklı örgü çözünürlüğü ile ve Elmer'in yeni cidar çözücüsü kullanılarak elde edilen doğal frekans değerlerinin (Hz) Afnor ve ticari bir yazılım ile karşılaştırılması.

5x örgüsü ele alındığında yeni Elmer çözücüsü, Afnor [1] verilerine nazaran %2,53(±0,17) hata oranına sahip sonuçlar üretmiştir. [Çizelge.1] üzerinde görüldüğü gibi Nastran sonuçlarının hata oranları çok daha düşüktür. Bununla birlikte Elmer sonuçlarındaki sapma frekanstan bağımsız olarak sabit bir seyir izlemekte, Nastran [2] sonuçları için ise frekans arttıkça sapma oranı giderek yükselmektedir. Bu sebeple çok daha geniş bantta bir karşılaştırma yapmak da ilgi çekici olabilir...

Aradaki sonuç farkının temel açıklaması olarak CQuad4 elemanının 404'e oranla, en azından bu problem için daha uygun olduğu düşünülebilir. Belki düz levhadan farklı olarak yüksek yüzey eğriliğine sahip bir cisim ile ikinci bir karşılaştırma yapmak da uygun olabilir.